覚えるだけで簡単に三平方の定理の計算問題が解けるよ。 覚えると便利!直角三角形の3つの比 それじゃあ早速、中学数学の問題でよく出てくる、 直角三角形の辺の比 を3つ紹介するよ。 比その1 「1 2 √3」 まず覚えておいておくべき直角三角形の辺の三平方の定理とは 直角三角形のときに利用できる 辺の長さの関係式でしたね。 それを発展させて考えていくと 直角三角形だけでなく 鋭角、鈍角三角形を見分ける方法として活用することができます。 入試などでは、活用する機会は少ないと思います直角三角形の3辺 の間に成り立つ関 係に着目し、操作や 実験等を通して共 通な性質を帰納的 に見いだすことが できる。 2 三平方の定理 の証明 三平方の定理の意 味や証明の仕方に 関心をもち、調べよ うとしている。 三平方の定理を演 繹的に証明するこ
Http Www Shimanet Ed Jp Minami Link Homepage Naga005 Pc Mathekyouzai001 Sanheihou Theorem Pdf
三平方の定理 直角三角形以外
三平方の定理 直角三角形以外-直角三角形の各辺の長さの関係はピタゴラスの定理(三平方の定理)と呼ばれる。 記号⊿を使ってあらわすことがある。 直角三角形の直角以外の2つの角を、直角三角形の鋭角 と呼ぶ。それらの大きさの和は、直角に等しい。 三平方の定理で直角三角形の辺の長さを計算してみると、 x² = 3² 5² x = √34 になるね。 答えが整数じゃなくてスッキリしないけど、こういう答えもありだ。




三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者
直角三角形の定義とさまざまな公式 レベル ★ 基礎 平面図形 三角比・三角関数 更新日時 直角三角形 とは,1つの角が直角である三角形のことです。 直角三角形のさまざまな性質を紹介します。 目次 三平方の定理(ピタゴラスの定理)右に直角三角形が描いてあります。 三平方の定理から、 z 2 = x 2 + y 2 が成り立ちます。 ですから、xyzの二つが分かっていれば、最後の一辺は、計算で出せますね。 でも、直角三角形でなければ、こうはいきません。 c 2 = a 2 + b 2 01ピタゴラスの定理(三平方の定理) 定理1(ピタゴラスの定理、三平方の定理) 直角三角形の斜辺の長さをa、そのほかの辺の長さをそれぞれb,cとすると、b²+c²=a²が成り立つ。 証明(これ以外にも様々な証明方法が存在する)
図2のように直角三角形(赤)をつくることができる。 斜辺が10cm, 残りの辺が8cmとxcmとして 三平方の定理にあてはめる。 100 = x 2 64 x 2 =36 x=±6 0電験三種の数学 三平方の定理の計算方法を押さえる 三平方の定理を使いこなして電気を簡単に扱おう 電験三種では、直角三角形をよく使います。 問題によっては直角三角形を書いて、それをもとに計算すると簡単に解けることがよくあります。直角三角形の計算には、三平方の定理 直角三角形以外の三角形の問題には正弦定理や余弦定理を使いますが、そこで出てくるsinAやcosBやtanC はどこを何を指してるんですか? 数学 三平方の定理を直角三角形以外の三角形に使う時の公式ってどうなりますか?
それで、三平方の定理を使えば、 2× 2 =√3×√3+ 1 × 1 になることは納得できます。 そのため、次の内容は正しいことになります。 3 つの辺が√3と 2 と 1 の三角形は直角三角形になり、内側の角度は 90 度、 60 度、 30 度になる このことは三平方の定理直角三角形だと,三平方の定理 が成り立つよね。 1番長い辺が斜辺になるんだね。 三平方の定理の逆が成り立つか ら,これは直角三角形だ。 三平方の定理を利用して,直角 三角形の辺の長さを求めること ができました。a2+b2=c2三平方の定理を使うと、直角三角形の 2 つの辺の長さからもう一つの辺の長さを求めることができます。 このページでは、三平方の定理を分かりやすく説明しています。中学校で学習する前の人にも、三平方の定理の意味を理解してもらえるような解説にしているので、ぜひお読みください。
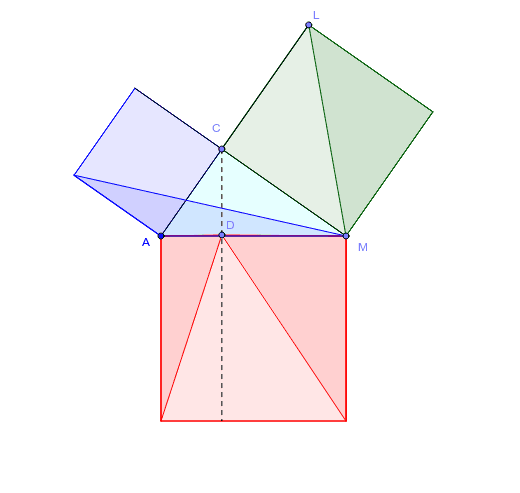



ピタゴラスの定理 ユークリッドの証明 Geogebra




勉強しよう数学 拡張三平方の定理
現在中学生ですが、三平方の定理を学校で習いました 直角三角形以外での求め方はないのだろうかと、いろいろ考えてみましたが、ぜんぜん分かりません 高校で習うのかもしれませんが・・・・ 二等辺三角形の場合だけとか、そういった限 では,例題のような「直角三角形ではない三角形 数学・算数 三平方の定理を使った問題 直角三角形ABCがあります。 斜辺の長さは2で、それ以外の辺を、 短いほうをx、長いほうをhとします。 さらに以下の条件が与えられていて、ここから 辺hの値を 質問No直角三角形の直角以外の2つの角を、直角三角形の鋭角 と呼ぶ。 三平方の定理で直角三角形の辺の長さを計算してみると、 x² = 3² 5² x = √34 になるね。 答えが整数じゃなくてスッキリしないけど、こういう答えもありだ。 Step3



3




三平方の定理を使うのか 比の計算をするのか 見極め方がよくわかりません Clear
初等幾何学におけるピタゴラスの定理(ピタゴラスのていり、英 Pythagorean theorem )は、直角三角形の3辺の長さの関係を表す。 斜辺の長さを c, 他の2辺の長さを a, b とすると、定理は = が成り立つという等式の形で述べられる 。 三平方の定理(さんへいほうのていり)、勾股弦の定理(こう数学 解決済 教えて!goo三角形における三角比の値 ABCでcosB の値を求めよ。 という問題で,cosB =3/2 と答えてしまいました。 sinθ ,cosθ ,tanθ の定義通りにあてはめたつもりですが,答えが正しくありませんでした。



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス



三角比って直角三角形でなくても成り立ちますか 詳しく教えてください 三角 Yahoo 知恵袋
三平方の定理の逆 A B C c a b 一般に ABCで、 a2+b2=c2 ならば、 ∠C=90° 問5 次の長さを3辺とする三角形のうち、直角三角形はどれですか。 5㎝、6㎝、7㎝ (2) 5㎝、12㎝、13㎝ (3) 7㎝、10㎝、12㎝ (4) 2 ㎝、3 ㎝、5 ㎝



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス




三平方の定理で辺を求める Youtube




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集




三平方の定理 特別な直角三角形の3辺の比 中学数学 定期テスト対策サイト




三平方の定理 特別な直角三角形の3辺の比 中学生からの勉強質問 数学 進研ゼミ中学講座



三平方の定理を直角三角形以外の三角形に使う時の公式ってどうなりますか Yahoo 知恵袋




三平方の定理の証明と使い方




直角三角形の辺を求める Youtube



高校入試 英語 数学 三平方の定理の逆




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




職業訓練試験用対策 忘れた方 勉強方法が分からない方のためのサイン コサイン タンジェント 三角比 解説例題集 ふくなんログ
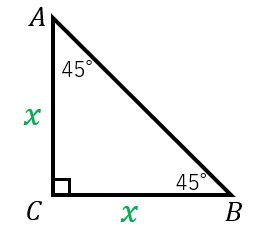



30 60 90 と 45 45 90 の直角三角形の辺の比 具体例で学ぶ数学




数学 中3 61 三平方の定理 基本編 Youtube
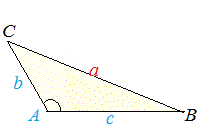



余弦定理




三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく




三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく




高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月



中学数学の最後にして最大の壁 三平方の定理はこれで満点ゲット 高校入試徹底対策ガイド



余弦定理の証明 公式の使い方を解説 センター過去問の解説付き Studyplus スタディプラス



図形問題です Abcは角度不明の直角三角形です 三平方の定理以外でabの長さ Yahoo 知恵袋



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者



6 改めてサンキュー 直角三角形 オトナのための中学数学 天狼院書店
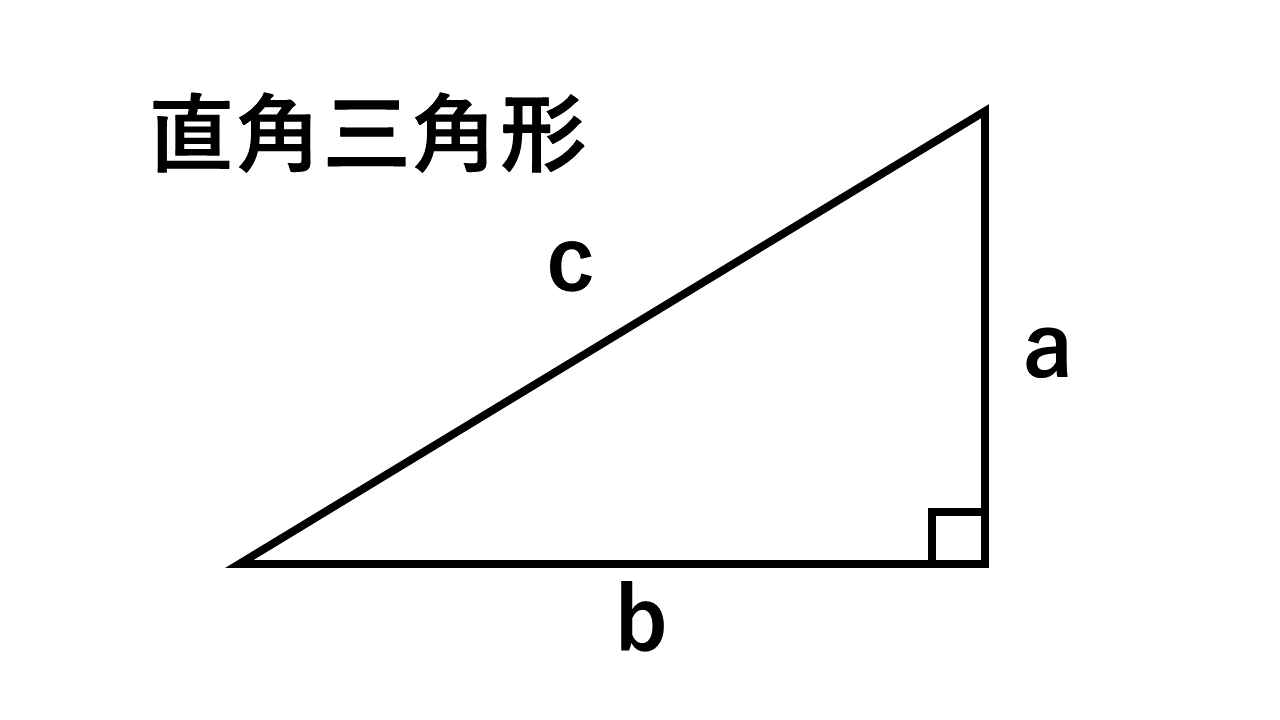



中学数学 直角三角形3 4 5以外に知ってる




三平方の定理の証明 直感的に分かる図で解説します 数学fun



三平方の定理 ピタゴラスの定理 の覚え方 八ヶ岳むらはま工房



直角三角形とは 定義や定理 辺の長さの比 合同条件 受験辞典



Http Www Shimanet Ed Jp Minami Link Homepage Naga005 Pc Mathekyouzai001 Sanheihou Theorem Pdf




三平方の定理およびその逆 証明 理数系無料オンライン学習 Kori




三平方の定理を簡単に理解 更に理解を深めよう 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導




職業訓練試験用対策 忘れた方 勉強方法が分からない方のためのサイン コサイン タンジェント 三角比 解説例題集 ふくなんログ




高校数学 第2余弦定理 三平方の定理の一般化 と第1余弦定理の証明と利用 受験の月



数学のコツ 三平方の定理 個別指導ソラオトのスタッフブログ



1
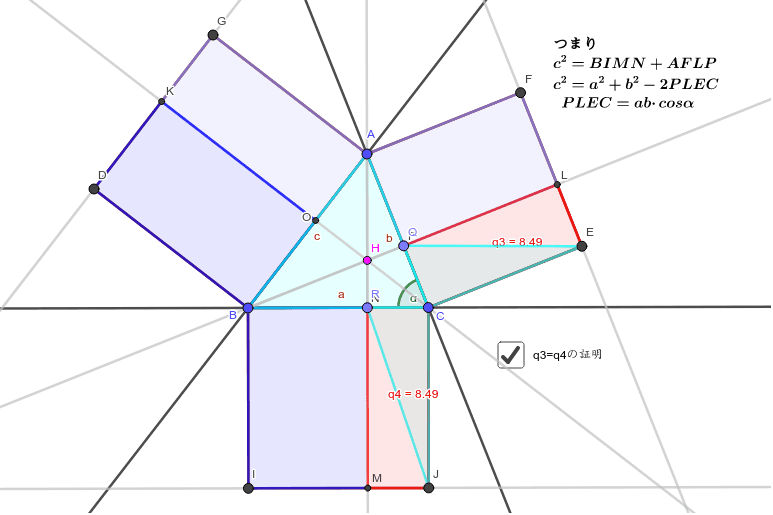



ピタゴラスの定理 ユークリッドの証明 Geogebra



中学数学の最後にして最大の壁 三平方の定理はこれで満点ゲット 高校入試徹底対策ガイド




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



三角比は直角三角形じゃないと定義できない 高校数学なんちな




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット



余弦定理とは 公式の覚え方や証明 計算問題の解き方 受験辞典




三平方の定理 特別な直角三角形の比を使った計算のやり方は Youtube




中学数学 三平方の定理 30 60 90 の直角三角形 オンライン無料塾 ターンナップ Youtube



友達が ピタゴラスの定理を使わずに直角三角形の斜辺以外の辺の長さを求められる Yahoo 知恵袋



Q Tbn And9gcsnbiv 7svsm 6o0qjqco66pmarde4rrmbqkrgwufvawvziomrf Usqp Cau
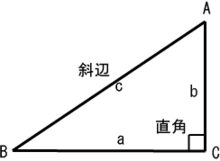



質問コーナー Discuss Scratch



三平方の定理とは 証明や計算問題 角度と辺の比の一覧 受験辞典




直角三角形の辺の長さ 合同条件 面積について アタリマエ
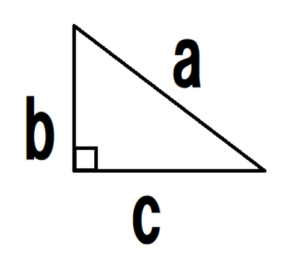



三平方の定理 公式を簡単に覚える方法 中学数学 札幌市 学習塾 受験 チーム個別指導塾 大成会




三平方の定理 チーム エン




簡単公式 直角二等辺三角形の辺の長さの2つの求め方 Qikeru 学びを楽しくわかりやすく



三平方の定理を使えば直角三角形以外の三角形も 二つの辺 Yahoo 知恵袋




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ



余弦定理を使えば直角三角形以外でもcos8の値が分かるというのであってい Yahoo 知恵袋




三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ
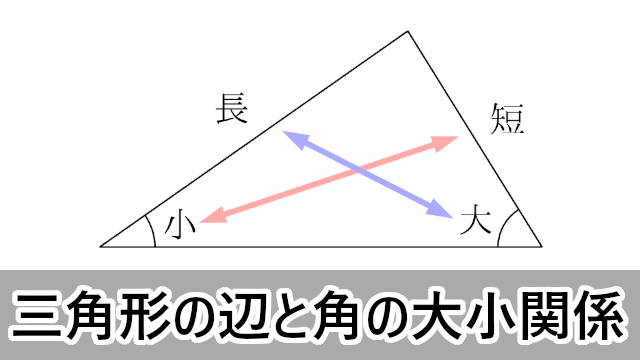



数学ia 三角形の角の大きさと辺の長さの関係 大学入試数学の考え方と解法
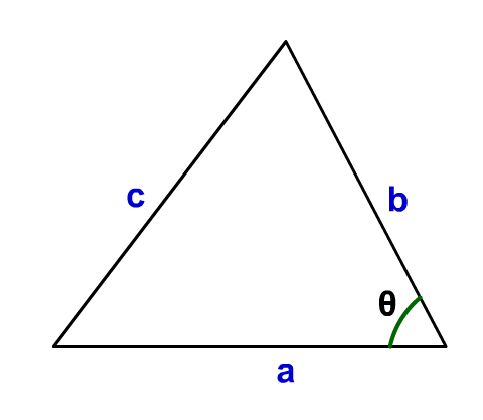



難しい 余弦定理 をシミュレーターを使って理解しよう 数学入門




最高のピタゴラス の 定理 直角 三角形 ページを着色するだけ




最高のピタゴラス の 定理 直角 三角形 ページを着色するだけ




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



Sin Cos Tanは直角三角形以外の三角形にも使えるのですか Sin C Yahoo 知恵袋




中3数学 三平方の定理 の重要ポイントをピックアップし 勉強方法を紹介 札幌市 西区 琴似 発寒 塾 学習塾 個別指導塾 マナビバ
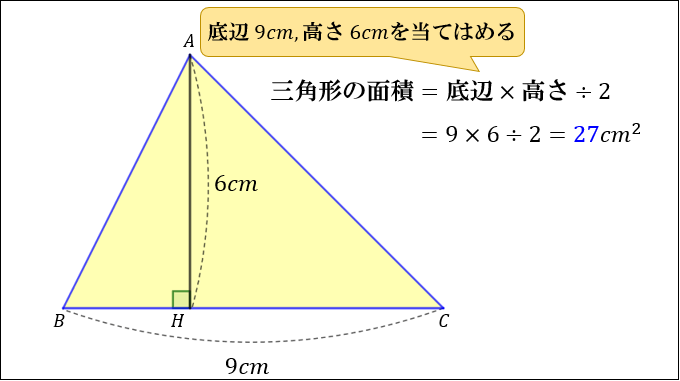



三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ




三平方の定理の証明と使い方




三平方の定理の計算 この問題は絶対にできるようになろう 中学や高校の数学の計算問題




三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく
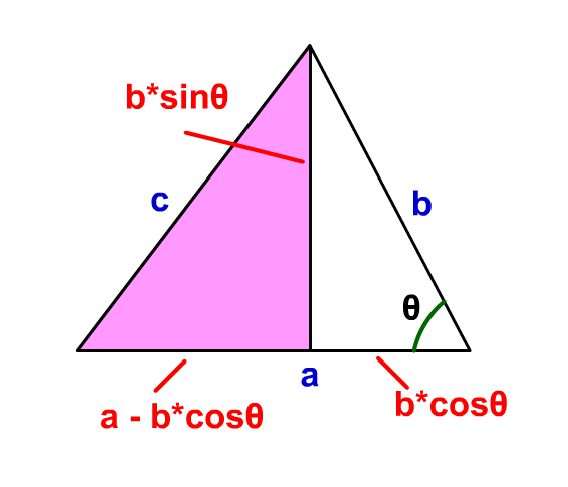



難しい 余弦定理 をシミュレーターを使って理解しよう 数学入門




3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく
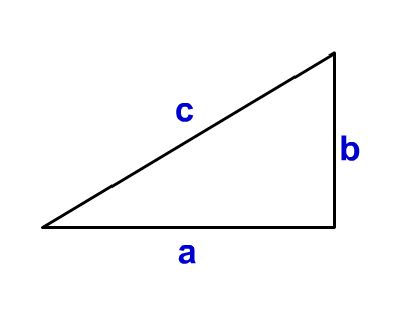



難しい 余弦定理 をシミュレーターを使って理解しよう 数学入門
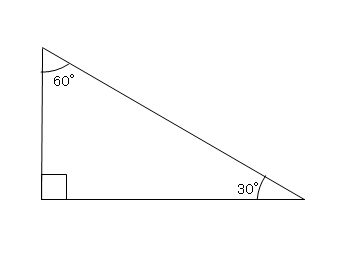



三平方の定理 特別な直角三角形 1 ネット塾




難しい 余弦定理 をシミュレーターを使って理解しよう 数学入門



三平方の定理とは 証明や計算問題 角度と辺の比の一覧 受験辞典
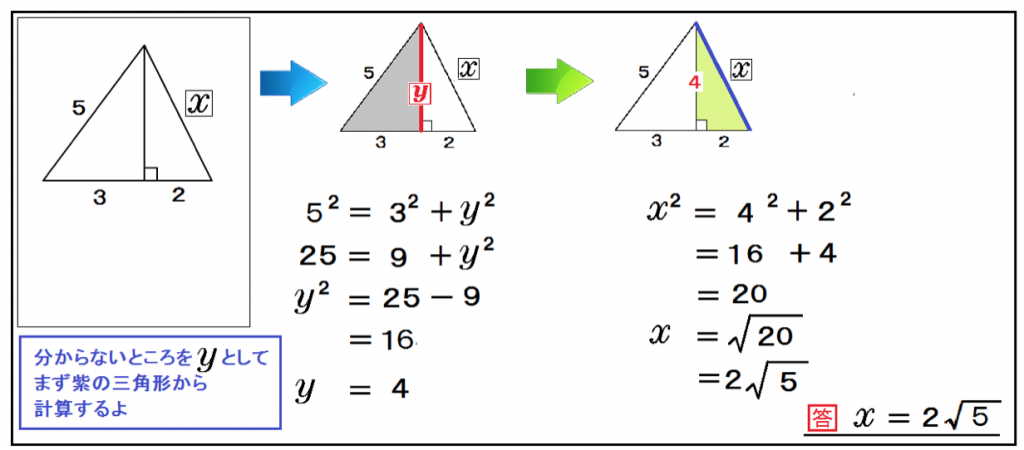



最高のピタゴラス の 定理 直角 三角形 ページを着色するだけ



直角三角形ではない場合ピタゴラスの定理はどう使えるのでしょうか Quora




最高のピタゴラス の 定理 直角 三角形 ページを着色するだけ




ガラパゴ数学 ますらば Ar Twitter 直角三角形の三辺を整数比 ピタゴラス数 にする式として A B 2ab A B というのがありますよね ガラパゴ数学ならビジュアルで説明可能です 同じ方法で直角三角形以外でも整数比を生み出す式を作れます 60 三角形 A B
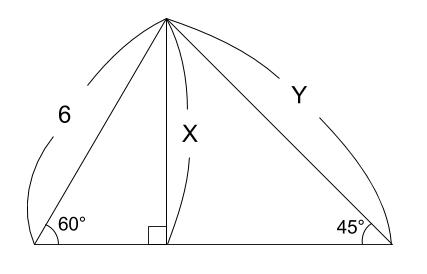



中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su
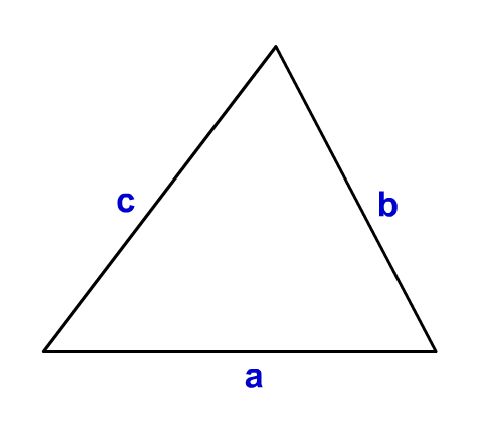



難しい 余弦定理 をシミュレーターを使って理解しよう 数学入門




難しい 余弦定理 をシミュレーターを使って理解しよう 数学入門



余弦定理の証明 公式の使い方を解説 センター過去問の解説付き Studyplus スタディプラス




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
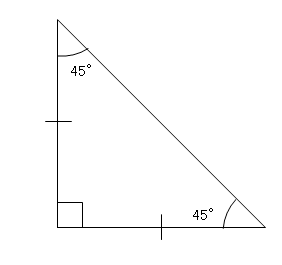



三平方の定理 特別な直角三角形 1 ネット塾



3
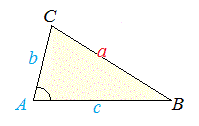



余弦定理




三角形の中の正方形の辺の長さを求める問題 X の長さを求めよという問題で Okwave




高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月




三平方の定理 ピタゴラスの定理 と公式の証明 忍者が用いた三角の知恵 アタリマエ




この公式は 直角三角形の時以外も使えるのでしょうか Clear




直角三角形の合同条件とその証明 数学fun




標準 2つの直角三角形に分解して三角比を求める なかけんの数学ノート



三平方の定理は直角三角形にしか使えないのですか 他の三角形でも使えそうに見え Yahoo 知恵袋
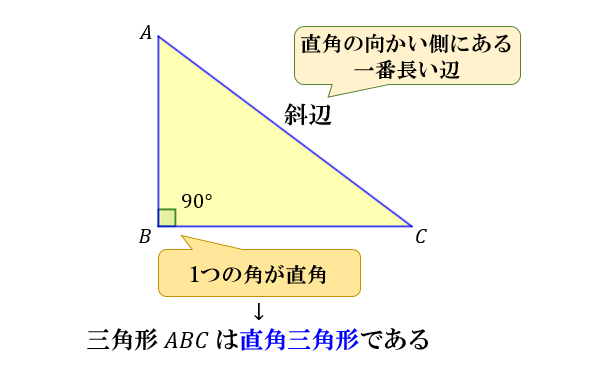



直角三角形の辺の長さ 合同条件 面積について アタリマエ
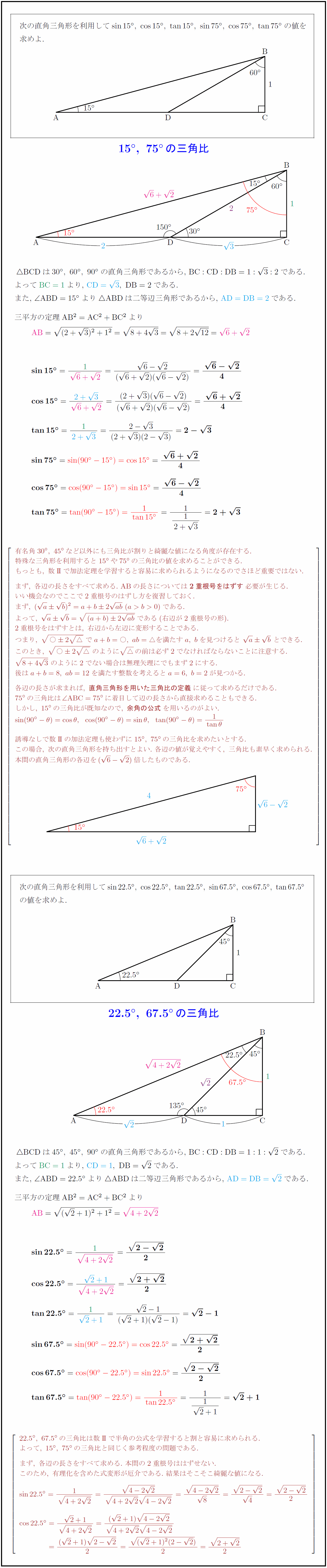



高校数学 15 75 22 5 67 5 の三角比の値の図形的な求め方 受験の月




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




コラム ピタゴラスの定理 江戸の数学




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




15 75 105 165 の三角比 数学i フリー教材開発コミュニティ Ftext


