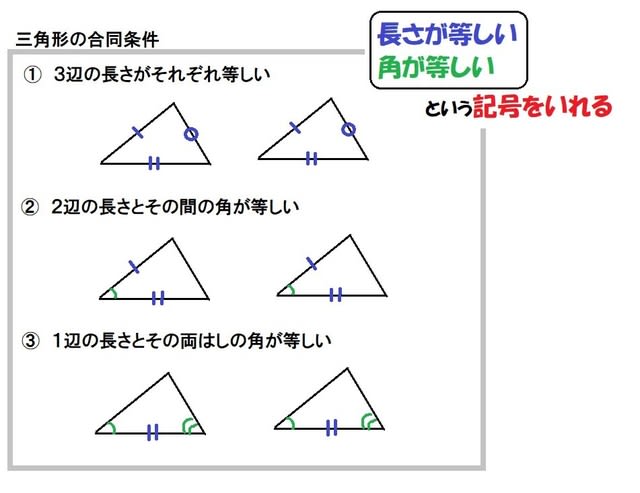
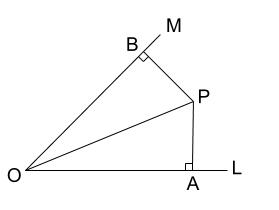
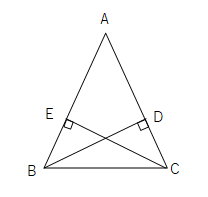
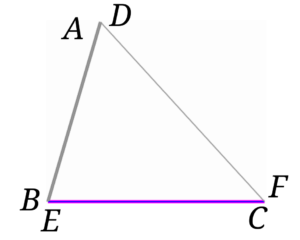
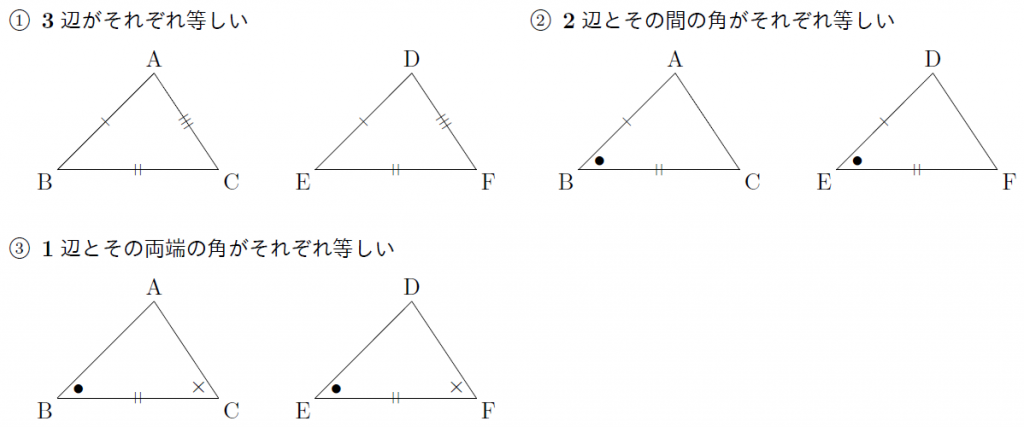
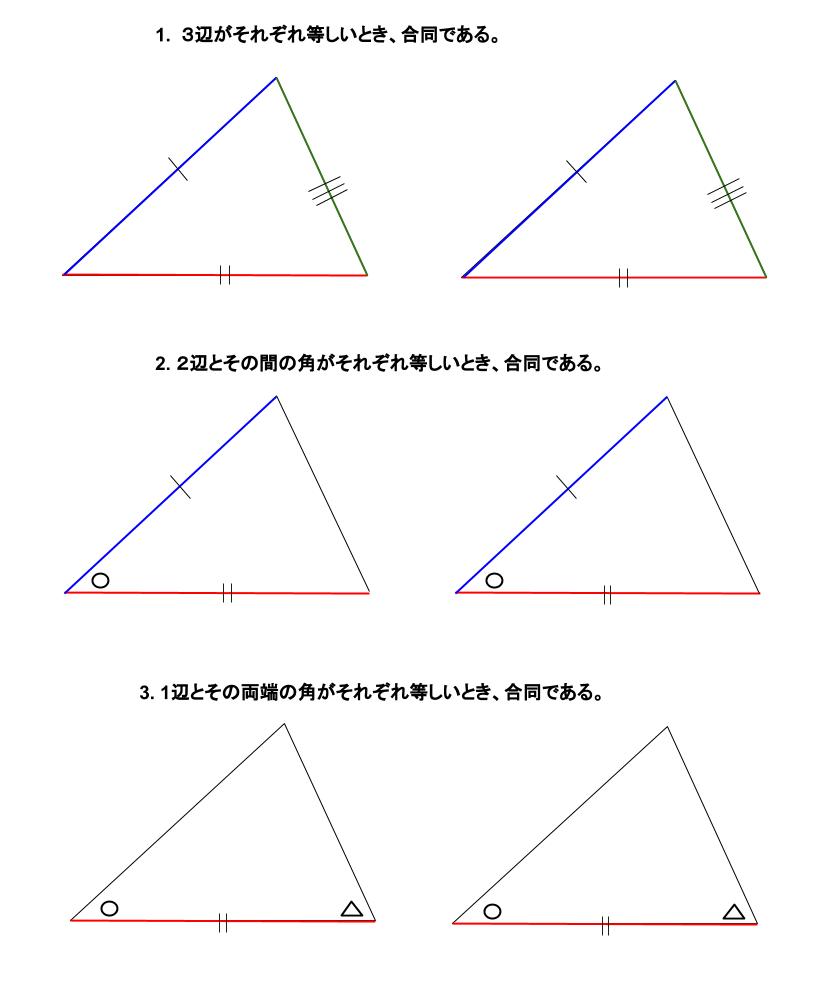
・証明の根拠としての基本性質を理解し、合同条件を用いて簡単な図形の性質を証明することができる。 3 評価規準 観点 評価規準 算数への関心・・三角形の決定条件を基に二つの三角形の合同となるための条件に関心をもち、考察しようとする。反応が予想されるが,その証明には直角三角 形の合同条件が根拠として必要である.既知 である一般の三角形の合同条件の限界を感じ させ,新たな知識の必要性につなげたい. 導入問題 右の図で 長さが等しい線分は あるでしょうか.合同とは 一方の図形を移動させて他方に重ね合わせることができる場合、この2つの図形は 合同 であるという。 三角形の合同を判断する場合、重ねあわせなくても下記の3つの合同条件のうちどれか一つに当てはまれば合同だといえる。 三角形の合同条件 3組の辺がそれぞれ等しい。 2組の辺とその間の角がそれぞれ等しい。 1組の辺とその両端の角がそれぞれ

中学2年生 数学 三角形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
合同の証明 条件
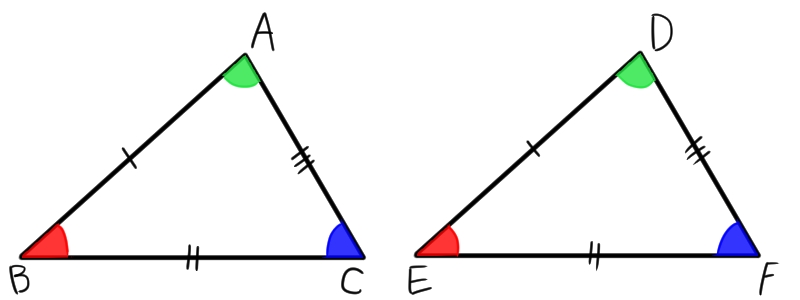
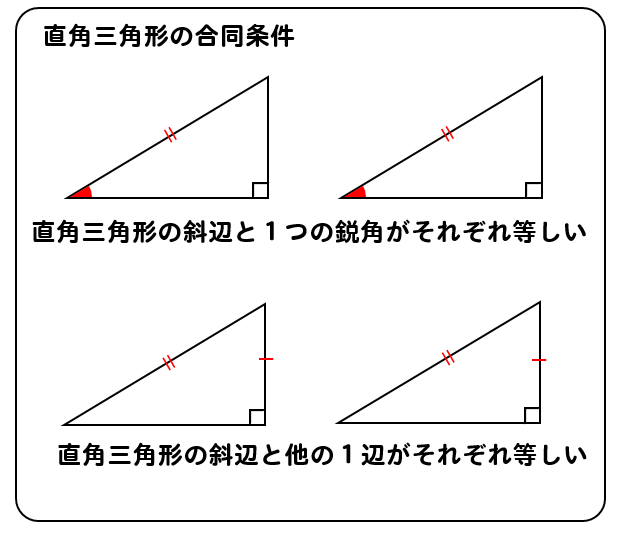
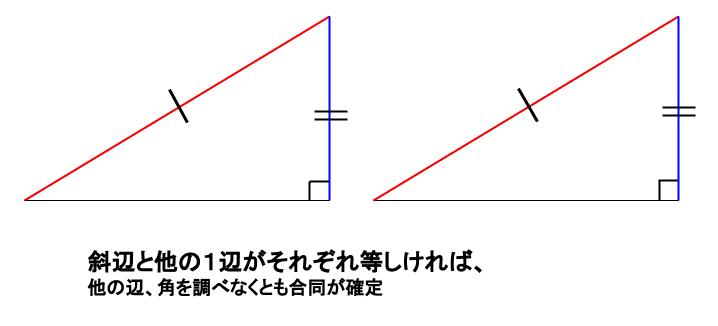
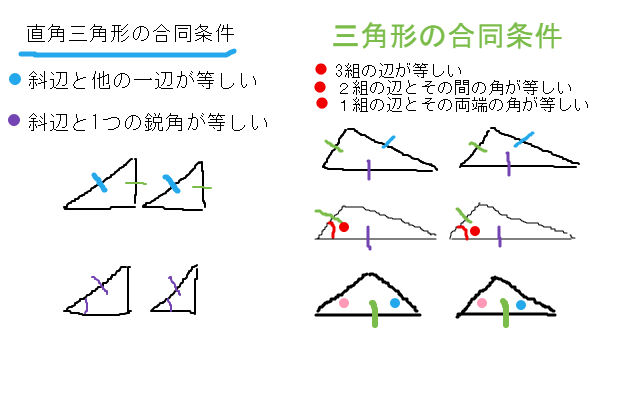
合同の証明 条件- を勉強してきたよね。 両方とも 数学の証明 のために必要なアイテムだから、テスト前には覚えなきゃいけないね。 念のためおさらいしておくと、 三角形の合同条件 3つの辺の長さがそれぞれ等しい 2組の辺の長さとその間の角が等しい 両端の角とその間の辺の長さがそれぞれ等しい 三角形の相似条件 3組の辺の比がすべて等しい直角三角形の合同条件 2つの直角三角形は、次の場合に合同である。 1 斜辺と1つの鋭角が、それぞれ等しいとき(証明) 2 斜辺と他の1辺が、それぞれ等しいとき(証明)



中2 数学 無料学習プリント教材
三角形の合同条件を使って、合同な三角形を見つける方法! 証明の書き方合同な三角形の証明問題の書き方を基礎から解説!←今回の記事 直角三角形証明問題の書き方とは?合同条件の使い方を徹底解説! 二等辺三角形の角度の求め方 厳選6問解説!三角形の合同条件がいえるようになると、新しい説明の根拠が増え、そ の後の証明でも多く活用できるため、丁寧に指導していく。 (2) 本校の2 年生では、中学校入学時に小学校の計算テストを行った。 証明問題は問題の作り方で、合同・相似条件を利用するものから、図形の性質を利用するものまで多種多様になってきます。 なので、およそ使われやすい条件や性質を挙げておきます。 3角形の合同条件 ①3辺のの長さがそれぞれ等しい。
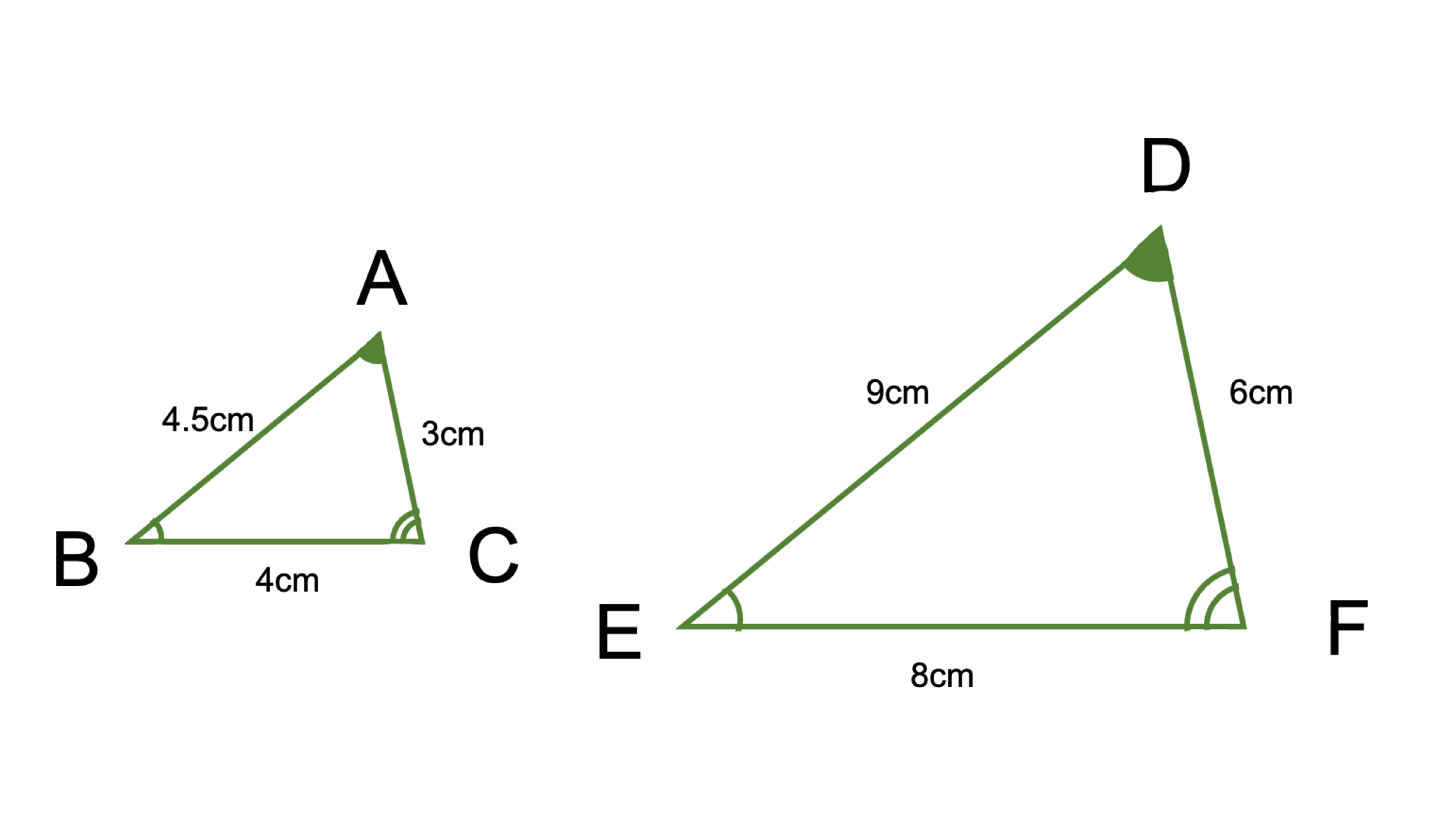
中学数学教科書「未来へひろがる数学」Q&A 三角形の合同条件の記述が,以前の教科書と変わっていますが,その理由を教えてください。 三角形の合同条件の記述 (2年p96)について,平成24年度教科書から次のように変更しております。 旧教科書 (1 三角形の合同条件の証明は? 「2つの三角形が合同条件を満たす→2つの三角形は合同」といえるのはなぜなのか? なぜあの3つの条件が合同条件に採用されたのか考えていきます。 2組の辺とその間の角がそれぞれ等しい。 の証明 A B C A B C と D E F D E F があります。 A B = D E A B = D E 、 B C = E F B C = E F 、 ∠ A B C = ∠ D E F ∠ A B C = ∠ D E F とします。 この2つの三角形が右図の abc と def が合同であることを証明した い。ab=de,bc=ef であることがわかっているとき, あと1 つ,どのようなことをつけ加えれば合同であるこ とが証明できるか。適切なものを次のア~エから2 つ選 び,記号を書け。
合同条件は3つとも必ず暗記するようにしてください! ※「合同」とは、全く同じ形をした図形のことです。つまり、三角形の合同条件とは、「2つの三角形が全く同じになるための条件」ということです。 合同条件① 合同条件の1つ目は、1 2組の向かいあう辺が、それぞれ平行である。 ( 定義 ) 2 2組の向かいあう辺が、それぞれ等しい。 ( 証明 ) 3 2組の向かいあう角が、それぞれ等しい。 ( 証明 ) 4 対角線が、それぞれの中点で交わる。 ( 証明 ) 5 1組の向かいあう辺が、等しくて平行である。証明 (合同・相似)が苦手な人へ 教遊者 IC Channel 192K subscribers Subscribe 中2,中3,受験生平行と合同,三角形と四角形,相似「証明 (合同・相似)が苦手な人へ90%以上の証明に使えるテンプレートと素材まとめ」デジタル板書データ Watch later




三角形の合同条件 証明のときに絶対にしておかないといけない問題 中学や高校の数学の計算問題



3分で分かる 三角形 直角三角形の合同条件とその使い方をわかりやすく 合格サプリ
三角形の合同条件、他にもある? 上の「3つの合同条件」の他に、「決まる!」場面はあるのでは? ① こちらの「3部分」でも「決まる!」 ・1辺が同じ ・どこか、2角が同じ (辺の両端でなくてよい?) しかし、2つの角が解れば、残りの角xも分かる 三角形の合同条件 三角形の合同を証明するためには、「合同条件」というものを使います。 一般的な三角形の合同条件は次の \(3\) つです。 条件①3 組の辺がそれぞれ等しい \(3\) 辺の長さがそれぞれ等しければ、合同と言えます。この活動を通して、合同条件に必要な三つの要素を意識 させ、記号を使って書き表す力を養う。 次に、三角形の合同の証明について書き方を学習する。仮定から合同条件の3要素でわかっている ものと足りないものを認識することで、合同条件を考える。




中学校数学 証明のコツ 直角三角形の合同条件 と その利用の仕方 を自学自習できる教材



1
三角形の合同条件の証明方法を教えてください。お願いします。 三角形の合同条件の証明方法を教えてください。お願いします。 2つの三角形を abcと defとします。二辺夾角相等ab=de,ac=df,∠a=∠dだとしますア 平面図形の合同の意味及び三角形の合同条件を理解すること。 イ 証明の必要性と意味及びその方法について理解すること。 ウ 三角形の合同条件などを基にして三角形や平行四辺形の基本的な性質を論理的に確かめたり, 図形の性質の証明を読んで新た中2数学。2つの「辺の長さ」が等しいことを証明せよ。ヤバいこれも合同証明? それとも違うの? 図形はムズカシイ(ガクッ)倒れ込む中学生。立て、立つんだトォォォォ~ッ! オール5家庭教師、見参ッ! 証明問題はコツがある!(ビシッ)無料サイトだ。




二等辺三角形 直角三角形の定義 合同条件と証明問題 リョースケ大学



三角形の 合同条件 とは 直角三角形の2つも覚えて証明問題を攻略しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
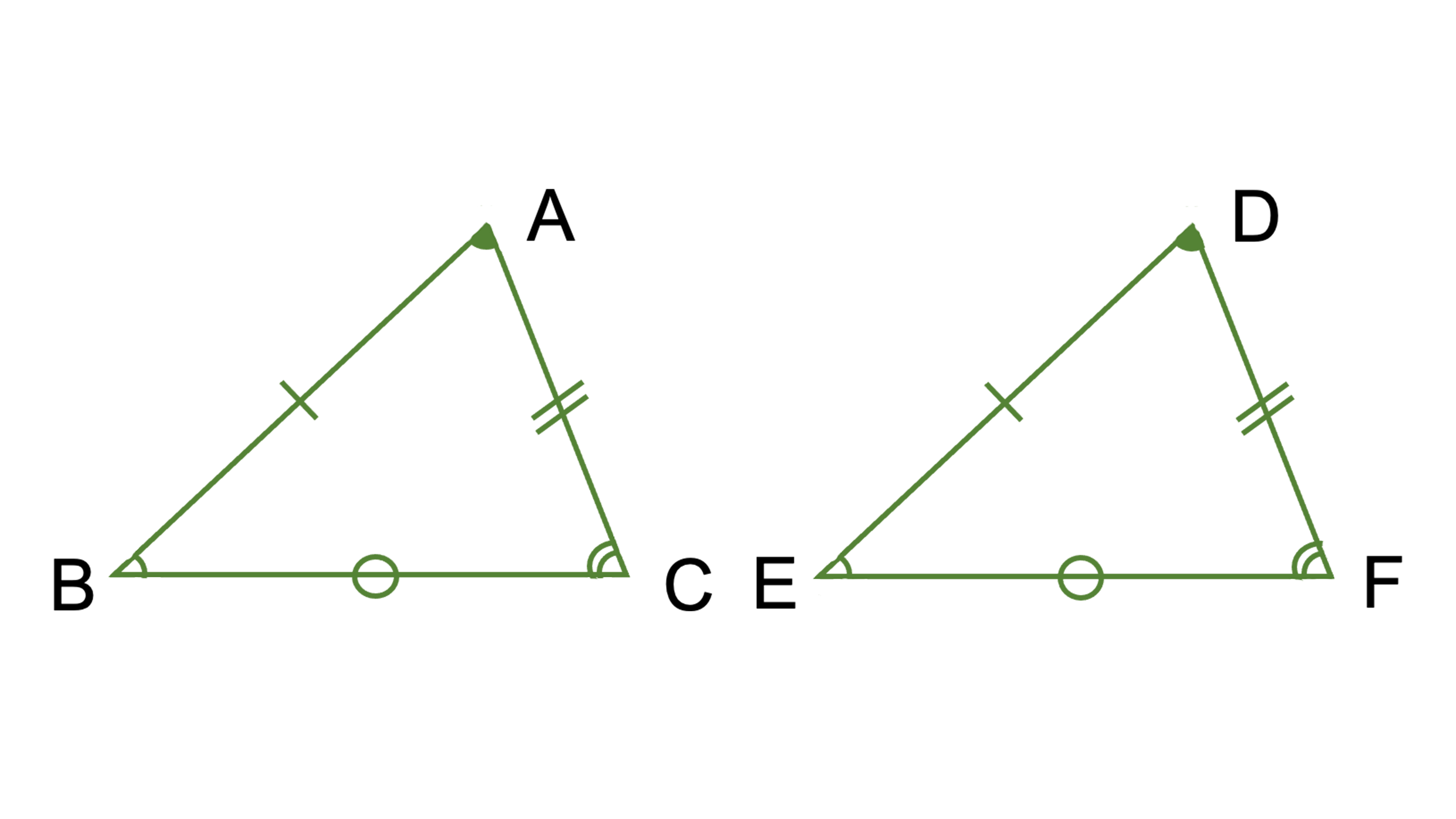
三角形の合同条件2(2辺とその間の角) step1 ポイント 三角形の合同条件2(2辺とその間の角) 中2数学で学ぶ「三角形の合同条件2(2辺とその間の角)」のテストによく出るポイントを学習しよう! step2 例題 三角形の合同条件2(2辺とその間の角) 中2数学で学ぶ「三角形の合同条件2(2辺とその間の角)」のテストによく出る問題(例題)を学習しよう! 三角形の合同証明の総合的な練習問題です。定期テスト対策や高校入試対策としてもご利用ください。三角形の合同証明のポイント基本的な合同条件、証明のやり方をしっかり確認してから取り組んでください。 三角形の合同 二等辺三角形 直角三角形1合同なることを証明する三角形を囲んで三角形の合同条件 本授業で証明するのは次の定理である。 定理a(3 辺相等の合同条件) 2 つの三角形において,3 組の辺がそれぞれ 等しいならば2 つの三角形は合同である。 4,5 では線分や角の加法・減法に関する 性質を考察した後に,定理aを証明している。



三角形の合同条件 合同な図形の見つけ方 証明問題の基礎を身につけよう 数スタ



合同な図形 小5 合同条件は超重要 算数の教え方教えますmother S Math Happy Study Support
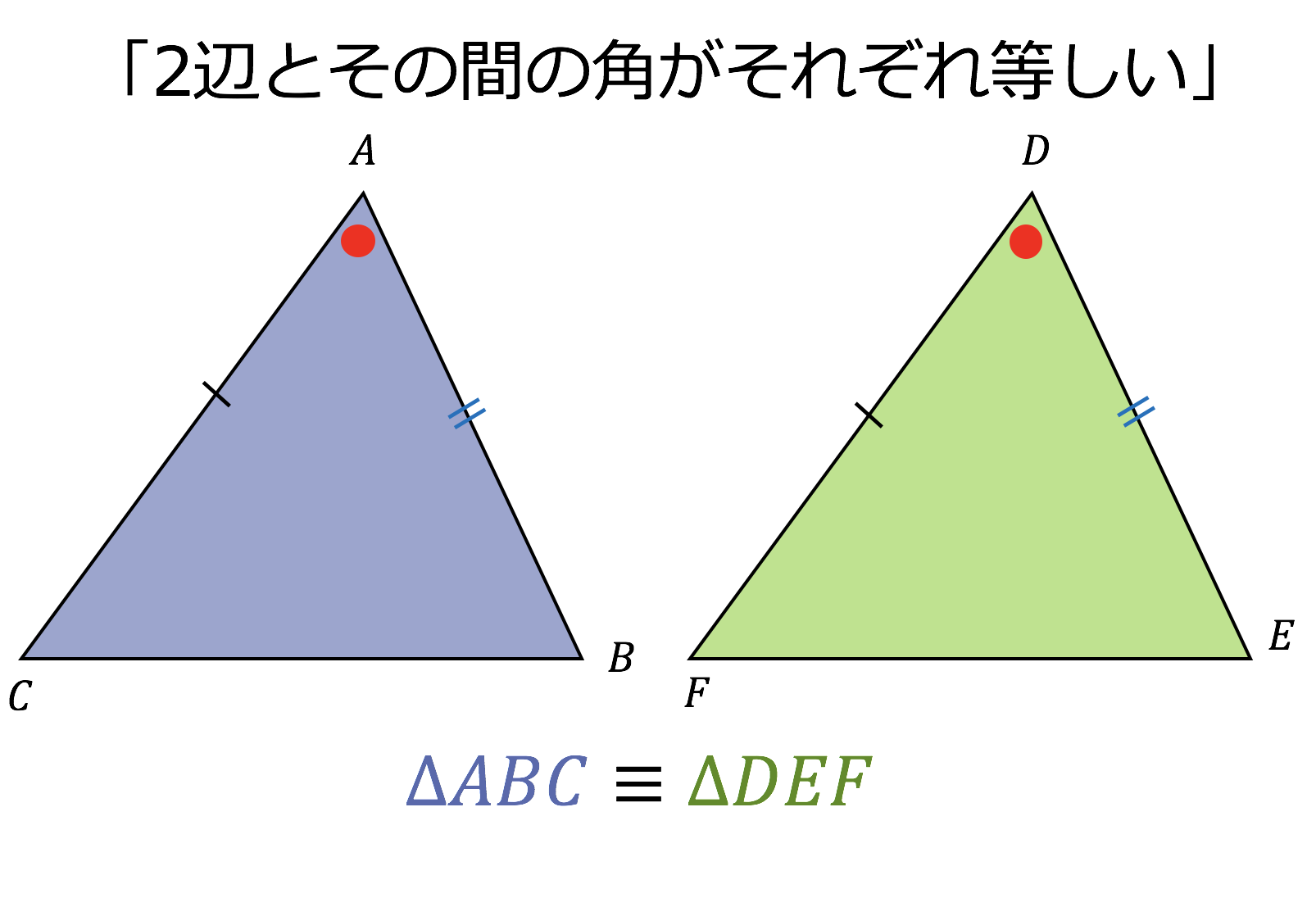
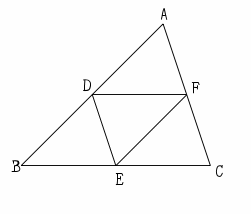
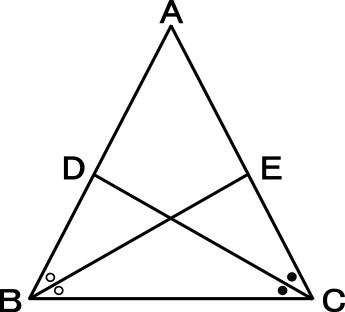
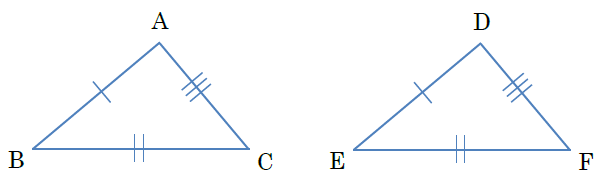
④合同条件(または相似条件)の3つからどれが当てはまるか を探っていきます。 もし、そこで条件が揃っていれば証明は出来ます。 これで解けるのは教科書範囲の問題が多いです。 入試問題では条件が1つ足りないことがよくあります。 そうなった場合は、仮定と,対頂角が等しいことを使って,合同条件に導く。 証明 ¼amcと¼bmdにおいて, 仮定より,am=bm ① cm=dm ② 対頂角は等しいから, −amc=−bmd ③ ①,②,③より,2組の辺とその間の角がそれぞれ等しいから, ¼amc×¼bmd a d b m c 確認問題三角形の合同条件 とは、 2つの三角形が合同であることを示すための条件 です。 以下の3つの合同条件のうち、どれかが成り立つ場合、その三角形は合同であるといえます。 3組の辺がそれぞれ等しい。 2組の辺とその間の角がそれぞれ等しい。




中2 数学 無料学習プリント教材




三角形の相似条件と証明問題の解き方 数学fun
「三角形の合同条件」の3つのうち、 2つに絞る ↓ 2.2つに絞った条件の、どちらかに合うような 辺や角を探す。(ただし仮定以外) この方法で考えると、 合同証明がもっとスムーズに 解けるようになります。 以下で、具体的な問題をお見せしましょう。 三角形の相似条件 相似の問題の中でも、三角形の相似を証明する問題が多く出題されます。 ここでは、三角形の相似を証明するために必要な3つの条件を説明します。 私が実際に問題を解いた時に使う回数が多いと感じた順に書いてみました。 1つめは、 「2組の辺の比とその間の角が等しい」 という条件です。 個人的には一番使う回数が多いと感じました辺=辺 ① 辺=辺 ② 辺=辺 ③ この条件を使う場合は、上記のように三組の辺がそれぞれ等しいことを例示して証明します。




直角三角形の合同条件を使った証明とは なぜ2つ増えるのか 遊ぶ数学



合同な図形 正三角形の証明問題 苦手な数学を簡単に
考察三角形の合同条件と合同の定義は同値なのか? 証明してみた 中学数学では三角形の3つの合同条件というものを習いますよね。 しかし、習った当時はひたすらに覚えろと言われ、理解せずにただ覚えた人が大半なのではないでしょうか合同の証明 証明とは 仮定や図形の性質を根拠として結論を導く。 等式を用いて説明するが、どの式にも 理由が必要 である。 三角形の合同を証明する 三角形の合同条件をそろえることで証明できる 例1 cはadの中点で, ∠bac=∠edcのとき bac≡ edcとなることを証明。 証明のポイント ①条件をすべて満たしていることを示す。 ②その根拠も必ず示す。 この二つのポイントがわかっていれば、図形の証明もばっちりです。 合同の証明をしてみよう では実際に合同の証明をしてみましょう。




中学2年生 数学 三角形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




三角形の合同の証明はとてもお得なんです セルモ大蔵 世田谷 の塾長ブログ



Www1 Gifu U Ac Jp Math Gifumathj Pdf



Http Www Fdtext Com Dat Suub2 4zukei 1kaku2 Pdf




三角形の合同条件 相似条件と合同条件の違いとは アタリマエ



フロー 2 5 4 4 直角三角形の合同条件を利用した証明



直角三角形の合同 証明問題 苦手な数学を簡単に




中2 数学 証明に使う条件 性質まとめ 中学生 数学のノート Clear



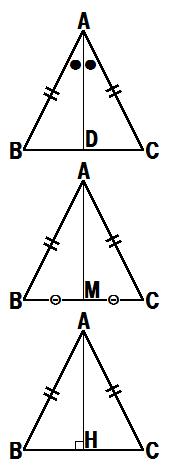
直角三角形の合同条件
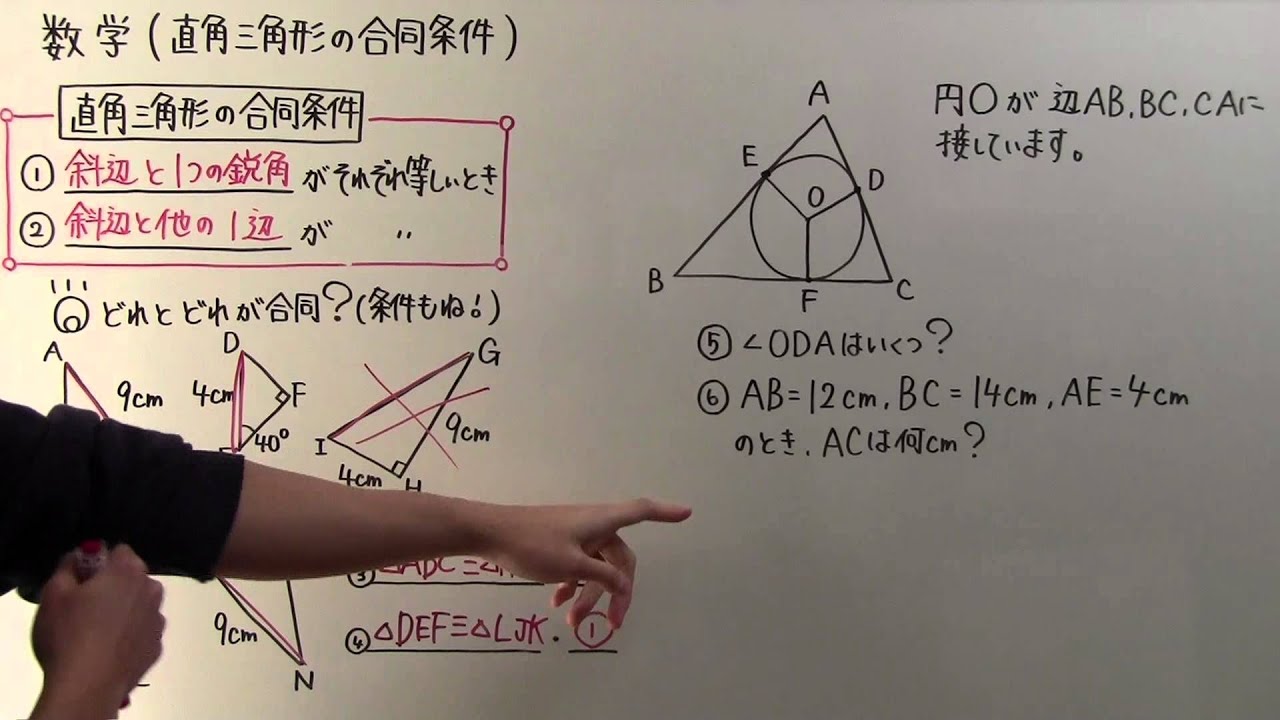



数学 中2 71 直角三角形の合同条件 Youtube
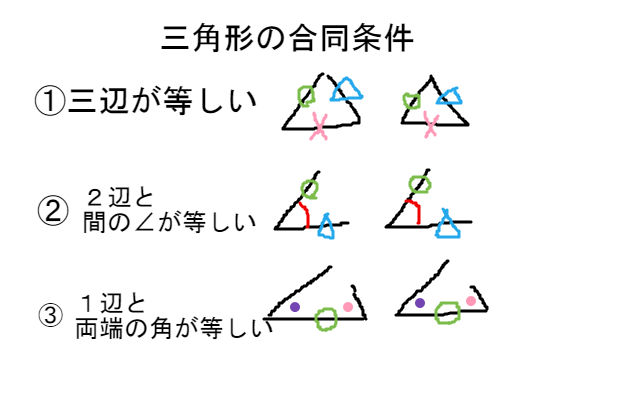



三角形の相似 合同条件 中学数学 理科 寺子屋塾の復習サイト




相似条件とは 三角形の相似条件はなぜ3つなの 証明問題アリ 遊ぶ数学
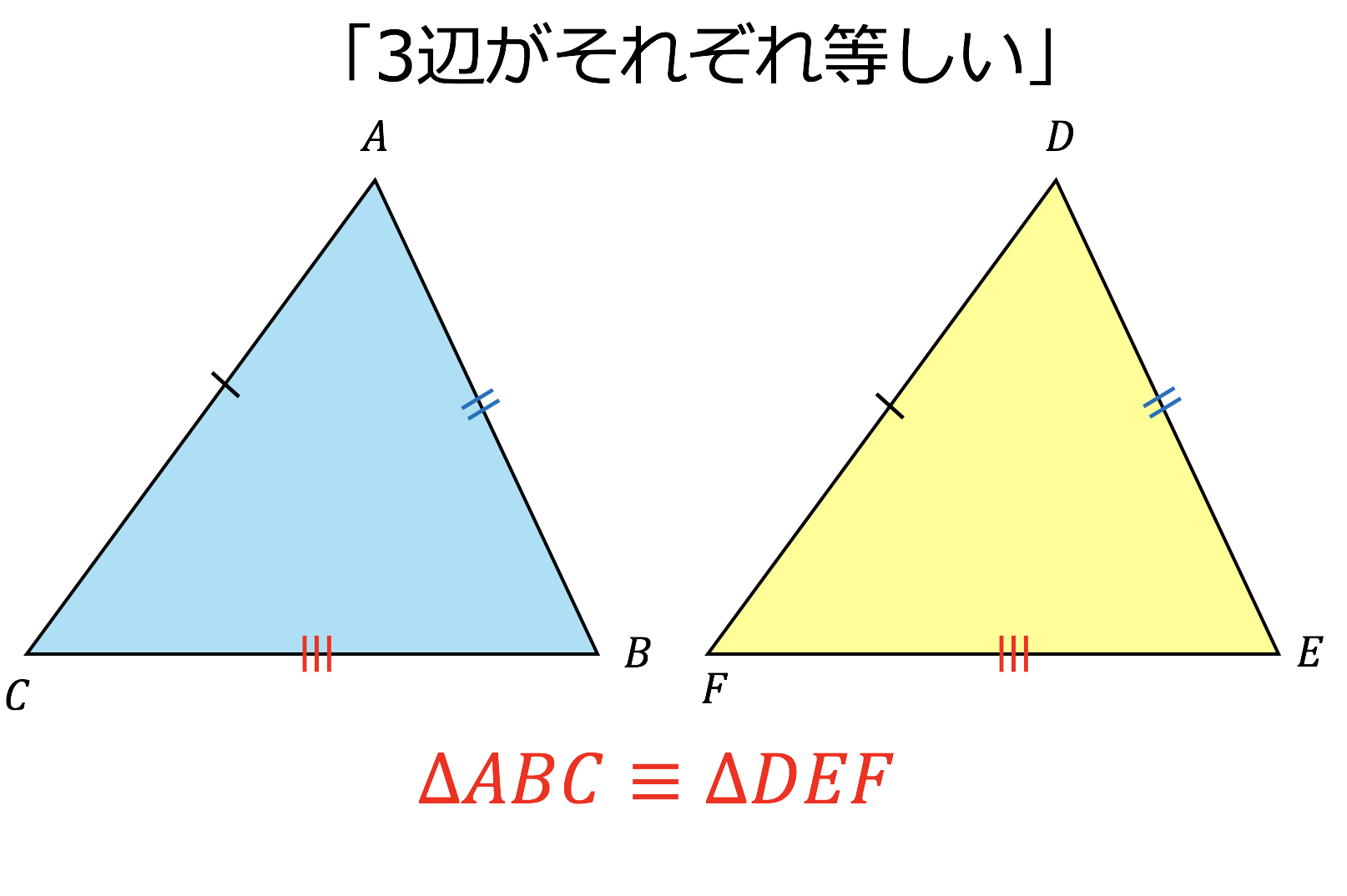



3分で分かる 三角形 直角三角形の合同条件とその使い方をわかりやすく 合格サプリ




相似の証明 チーム エン




5分でわかる 三角形の3つの合同条件 Qikeru 学びを楽しくわかりやすく




直角三角形の合同条件再び 中学校2年生の数学 身勝手な主張



中学数学証明問題です 直角三角形の合同条件はわかるのですが Yahoo 知恵袋




三角形の合同条件を使った証明問題 中学2年生の問題を解こう 身勝手な主張




暗記必須 三角形の合同条件を見やすい図で一発理解しよう 高校生向け受験応援メディア 受験のミカタ
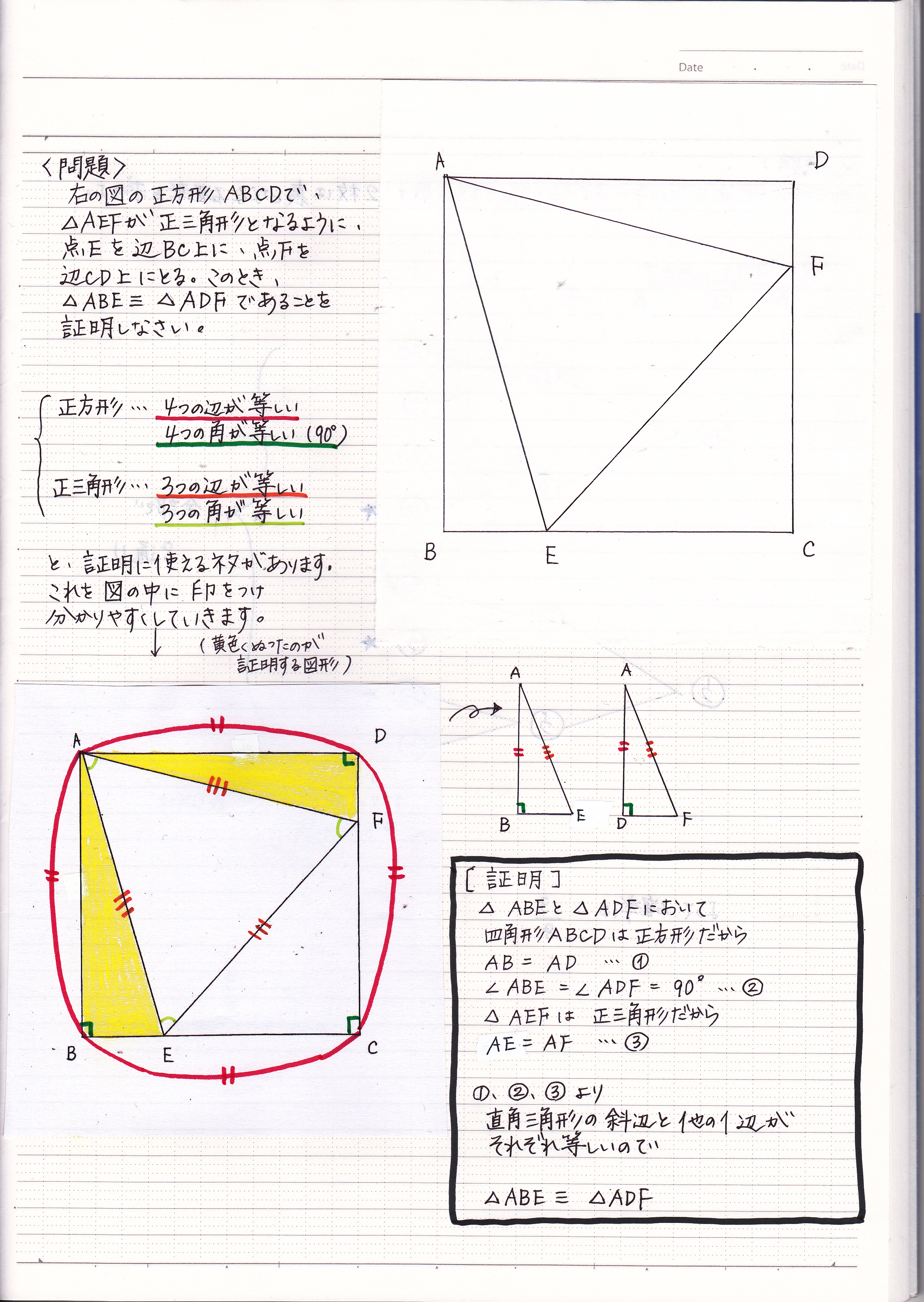



図形の証明 合同 現役塾講師のわかりやすい中学数学の解き方



中学数学 直角三角形の合同の証明 中学数学の無料オンライン学習サイトchu Su



中学2年生の数学 証明 三角形の合同条件と証明の書き方 塾講師が数学をやりmath




どの三角形の合同を証明すべきか 17年度北海道 高校入試 数学 良問 難問




三角形の相似条件 証明の練習になる簡単な問題を紹介 中学や高校の数学の計算問題




直角三角形の合同条件とその証明 数学fun



合同とは 三角形の合同条件 証明問題をわかりやすく解説 受験辞典




二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者



三角形の合同条件を図で分かりやすく説明 具体例で学ぶ数学




三角形と四角形 三角形の合同の証明のしかた 中学数学 定期テスト対策サイト



直角三角形の合同条件 証明問題の書き方とは イチから徹底解説 数スタ



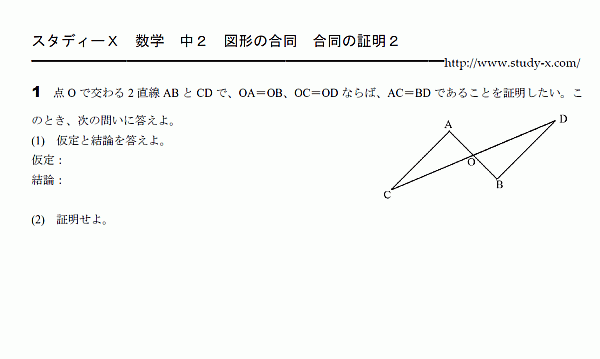
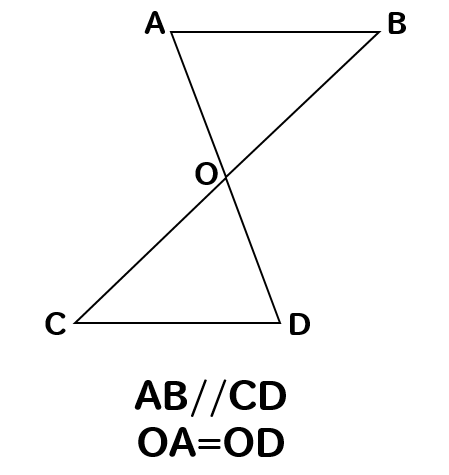
合同の証明2



三角形の合同条件と二等辺三角形の底角 2 算数 数学記事



三角形の合同条件3辺 Geogebra




二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者




二等辺三角形になることの証明 Youtube



中学生です 数学について三角形の合同 相似の証明のための合同条件や直角三角形 Yahoo 知恵袋



1
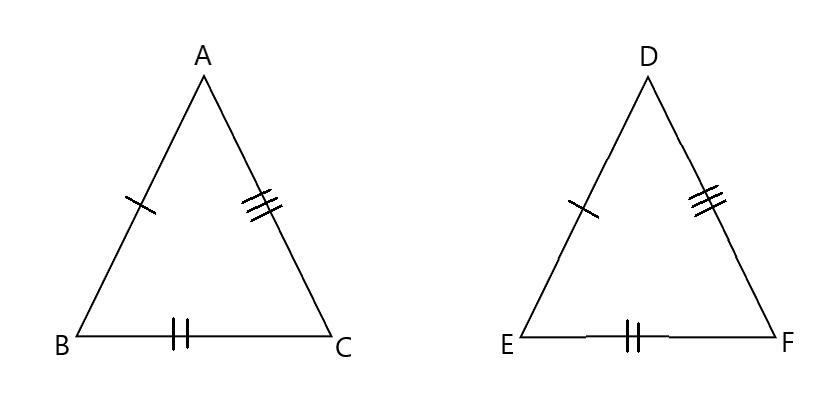



合同と相似とは 演習問題にチャレンジ 個別指導のオンライン家庭教師wam



中2数学 直角三角形の合同の証明のポイントと練習問題 Pikuu




合同と証明 Ict教材eboard イーボード



Www1 Gifu U Ac Jp Math Gifumathj Pdf



三角形の 合同条件 とは 直角三角形の2つも覚えて証明問題を攻略しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード



中学数学 三角形の合同の証明 その2 中学数学の無料オンライン学習サイトchu Su




中2数学 三角形の合同を証明する問題 練習編 映像授業のtry It トライイット



中学2年数学練習問題 図形と合同 三角形の合同の証明問題




2 の直角三角形の合同条件は何ですか 理由も付けて教えて頂けると助かります Clear
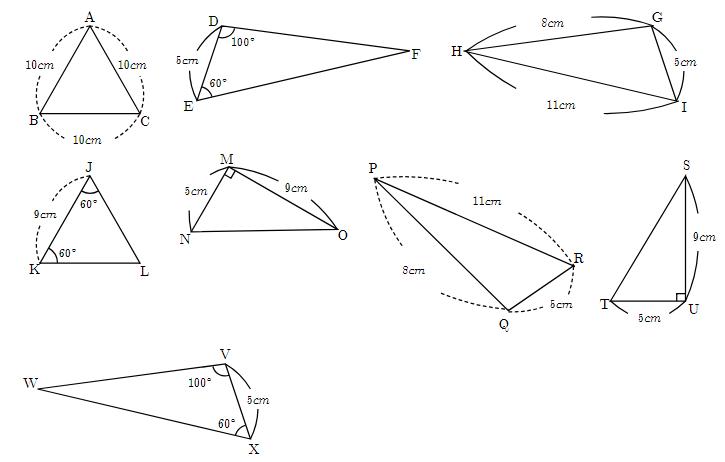



中2数学 三角形の証明の仕方 Pikuu




世界一わかりやすい数学問題集中2 4章 平行と合同と証明




三角形の合同条件 小学生 中学生の勉強




三角形の合同条件 Youtube



Studydoctor三角形の合同証明の進め方 中2数学 Studydoctor
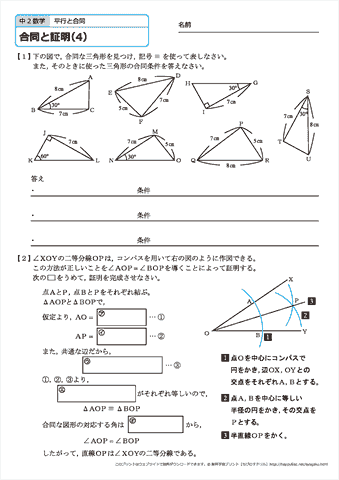



中学2年生 数学 合同と証明 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
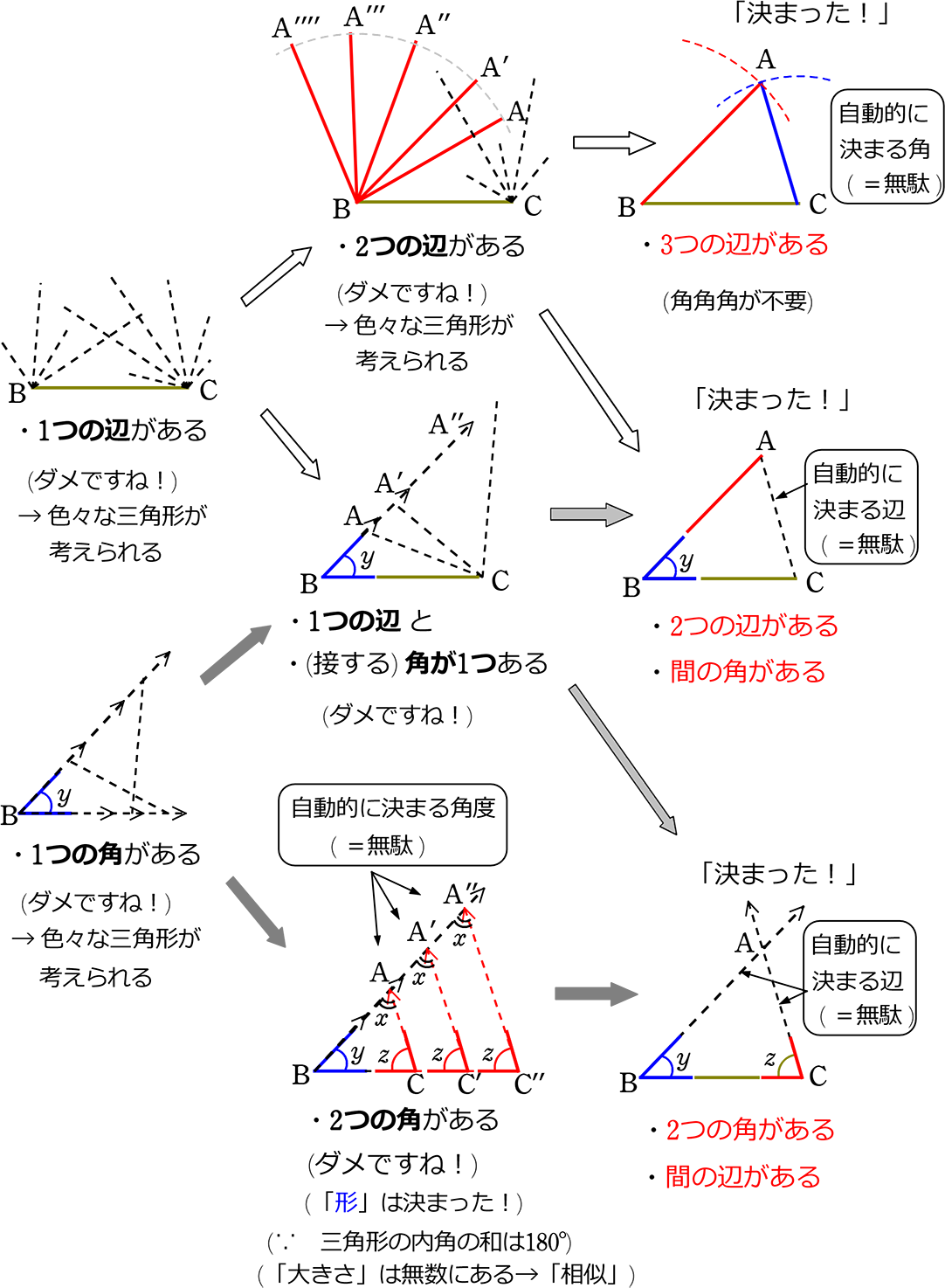



中学数学 図形の合同 図形の性質




中2数学 三角形の合同の証明の解き方の手順 こいがくぼ翼学習塾




中2数学 三角形の合同条件2 2辺とその間の角 練習編 映像授業のtry It トライイット




直角三角形の合同条件 証明のときに直角三角形が出てきたらこれ 中学や高校の数学の計算問題
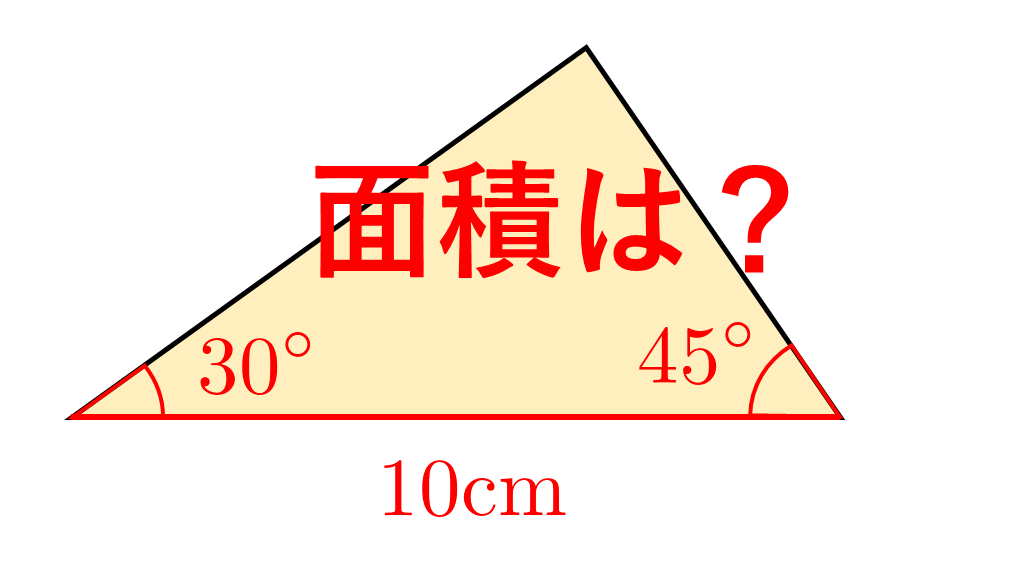



三角形の合同条件と面積 数学 統計教室の和から株式会社




三角形の合同条件はなぜ3つ 証明問題をわかりやすく解説 相似条件との違い 遊ぶ数学
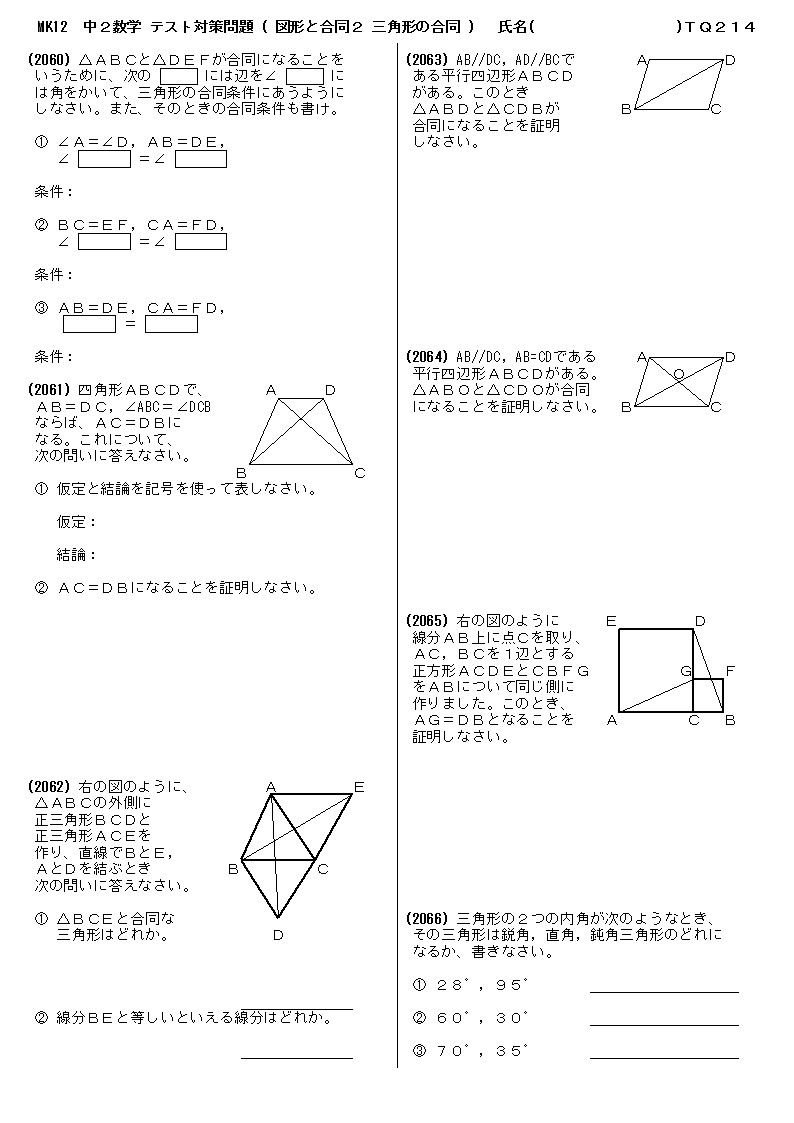



無料 中2数学 テスト対策 問題プリント 214 図形と合同2 三角形の合同
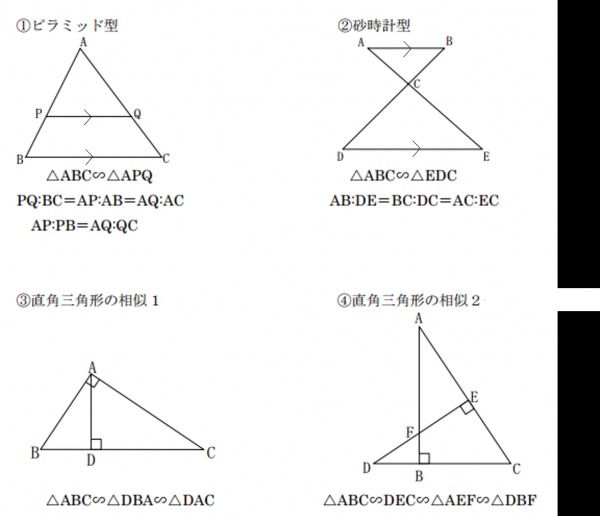



三角形の相似 合同条件 優技録




三角形の合同条件 合同の証明問題と解き方のコツ リョースケ大学




世界一わかりやすい数学問題集中2 5章 図形の性質と証明




中学数学より3 三角形の合同条件 身勝手な主張
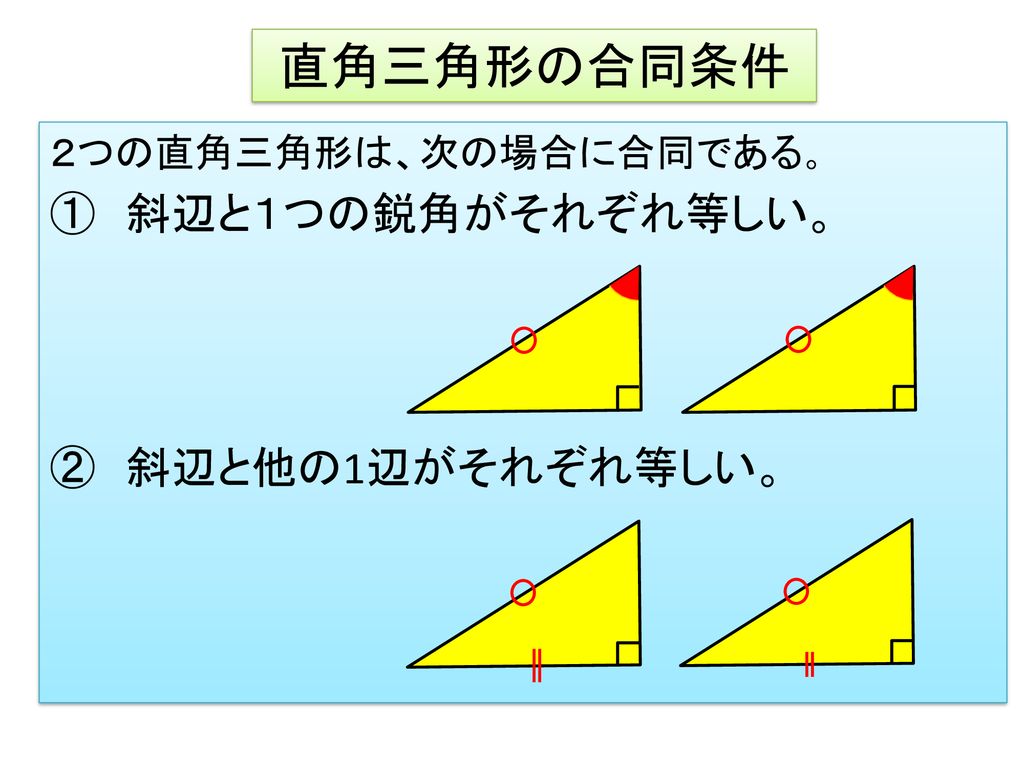



本時のねらい 直角三角形の合同条件を導き それを理解し 証明ができるようにする Ppt Download




直角三角形の合同条件を使った証明問題の解き方 現役塾講師のわかりやすい中学数学の解き方



中2数学 発展問題プリント12 図形6 証明のしくみと根拠 問題 226




三角形の合同条件



Studydoctor三角形の合同の証明 応用 中2数学 Studydoctor
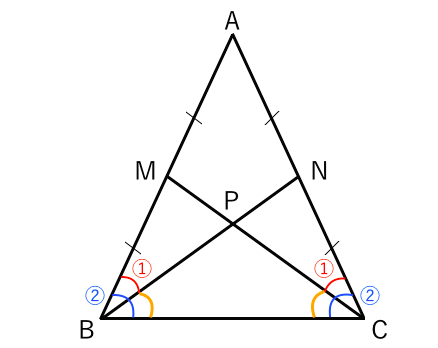



合同な図形 二等辺三角形の証明問題 苦手な数学を簡単に




三角形の合同条件と証明問題の解き方 数学fun



合同 相似条件の書き方 中学から数学だいすき



直角三角形の合同条件とそれを利用した証明 チーム エン



三角形の 合同条件 とは 直角三角形の2つも覚えて証明問題を攻略しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード



三角形の合同条件の表現ってなぜこの3つなの まぜこぜ情報局




合同と証明 Ict教材eboard イーボード



中学数学 直角三角形の合同条件 中学数学の無料オンライン学習サイトchu Su




中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン




三角形の合同条件はこれで完璧 必ず覚えておくべき3つの条件



中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン




二等辺三角形の定理の証明がわかる3ステップ Qikeru 学びを楽しくわかりやすく




中2数学 平行四辺形の証明で知っておくべき5つの方法 映像授業のtry It トライイット



三角形の合同条件 まなびの学園



中学数学 三角形の合同条件 中学数学の無料オンライン学習サイトchu Su



三角形 合同 相似条件 直角三角形の合同条件 中学数学 理科 寺子屋塾の復習サイト




数学 中2 56 三角形の合同 基本編 Youtube




三角形の合同条件
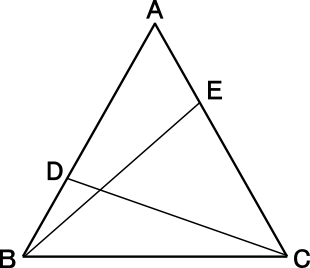



中学2年数学練習問題 図形の合同条件と証明の進め方の解答
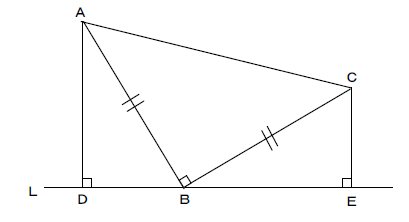



中2数学 直角三角形の合同条件を使った証明の定期テスト過去問分析問題 Atstudier



1



1
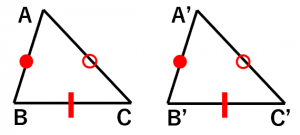



三角形の合同条件を図で分かりやすく説明 具体例で学ぶ数学



中2数学 直角三角形の合同条件と証明問題 授業わかるーの Byナオドット先生 中学数学のわかりやすい解説サイト


